在前面中介绍了信号完整性分析所采用的工具,其中之一是建模。在这里就要利用这个分析工具,首先为传输线建立模型,然后分析它的各种行为特征。
传输线的零阶模型是最简单且最易理解的模型,如图1所示。它是由一排微型电容并联组成,数值上等于传输线每一单位长度的电容量。

图1 传输线的零阶模型
下面介绍如何用传输线的零阶模型来分析传输线的电压-电流(V-I)特性和瞬态阻抗。
设单位长度为△X,每个微型电容的大小就是传输线单位长度的电容量气与单位长度的乘积:
C=Co×△X (3-5)
电流I由注入到每个电容上的电量Q决定,注入电容的电量Q等于电容C乘以其两端的电压V。电量注入到每个微型电容的时间间隔为△t,等于单位长度△X除以信号的传播速度υ。可以用下面的式子表示电流I:

可以看到,导线上的电流仅与单位长度的电容量、信号的传播速度和电压有关。传输线的电压-电流(V-I)特性:传输线上任何=处的瞬时电流与电压成正比。
得到传输线的电流后,可以推导出信号受到的瞬态阻抗,根据欧姆定律
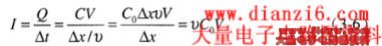
实际计算中υ取材料中的光速带入上式可得

由上式可知,传输线的瞬态阻抗只由传输线的横截面积和材料特性即介电常数共同决定,单位是Ω。
例:若介电常数为9,单位长度电容气为4.98 pF/in,那么传输线的瞬态阻抗为

如果传输线的以上两个特性参数保持不变,无论传输线的长度如何变化,瞬态阻抗始终是一个定值。
零阶模型把传输线描述成-系列间隔一定距离的微型电容的集合,这仅是传输线的物理模型,为了得到其等效的电气模型,接下来介绍传输线的一阶模型。
一阶模型是建立在零阶模型的基础之上,把传输线的两条导线的每一小段用电感代替,每两个并联的微型电容由电感连接,共同组成了一个微段,如图2所示。

图2 传输线的一阶模型
经典的传输线分析理论的基本思想是:均匀传输线的各电路参数均匀地分布于传输线上,因而传输线上的电压不仅是时间t的函数,而且是空间坐标x的函数,即
在距离始端x处取长度为曲的微段来研究,当dx足够小时可以忽略该段上电路参数的分布性,用集中参数电路来等效代替,这样,整个均匀传输线可以视为由一系列这样的微段级联而成。由于牵涉到微分方程,从实用的角度出发,在这里就不作介绍了,读者可以参考相关传输线理论的文献。
为了简化对一阶模型的分析,假设电容和电感无穷小;LC电路的节数趋于无穷;单位长度电容Co和单位长度电感Lo都为常数;传输线的总长为ι;那么总的电容和电感分别为
C=Co×ι (3-11)
L=Lo×ι (3-12)
由特征阻抗Zo和速度v推导单位长度电容和单位长度电感如下

传输线时延和特征阻抗推导总电容和总电感如下

由网络理论可知,信号沿网络传输时,在每一节点上都受到了恒定的瞬态阻抗,并且信号经输入网络到输出网络会存在一定的时延。式(3-13)和式(3-14)就能支持这一结论的成立。
为了避免烦琐的理论和微分方程推导,再给出一些关于一阶模型的实用计算公式,便于读者今后查阅。
以上介绍的这些关系式适用于所有的传输线,并且与其几何形状无关。如果知道其中的两个,就可以求出其余所有的参数,非常便捷实用。
,PCB传输线模型